| Introduction |
Structure
| |||||||
Les matériaux de construction
| |||||||
Etude des forces
|
Les contraintes
|
| Conclusion |
| Bibliographie |

Etude des forces :
Les types de forces
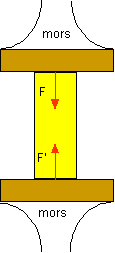
Forces de compression : c'est la force qui tend à écraser ou à rapetisser le matériau sur lequel il agit. Par exemple, sur les piliers, ce sont elles qui permettent de supporter l’ensemble du poids du pont. Si la force de compression est trop grande, le matériau se compresse. C'est ce qui se passe lorsqu'on écrase une colonne de pâte à modeler avec nos mains. Exemple d'un solide compressé dans un étau :
-les forces F et F' sont égales Force de tension : c'est la force qui tend à étirer ou à rallonger le matériau sur lequel il agit. Si la force de tension est trop grande, le matériau fendra. C'est ce qui se passe lorsqu'on étire une colonne de pâte à modeler avec nos mains, il se fait de petites "crevasses" sur la surface. elles s’exercent sur les câbles porteurs du pont suspendus, la somme de ces forces est égale au poids du tablier et des voitures passantes. Ce sont des forces d’interaction, elles ont donc même direction même valeur mais des sens opposés. Il ne faut négliger l'importance d'avoir plusieurs haubans qui permettent une meilleure répartition des forces sur le pilier et sur le tablier et ainsi assurent une certaine sécurité au cas où un ou plusieurs câbles lâcherait. La valeur de la force est répartie proportionnellement sur chaque câbles, donc plus il y a de câbles, moins la force supportée par chaque câble est grande.
- Les normes F et F' sont égales
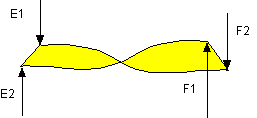
Force de torsion : Il s’agit d’une force qui tend a tordre latéralement le tablier, en cas de conditions climatiques particulières, comme un vent violent.
Le tablier ne subit aucune force
Le tablier subit les forces F1, qui soulève le tablier, et F2 qui appuie dessus. Les points E1 et E2 sont des points d’attaches qui sont reliés au pylône.
Le poids du tablier : Le poids du tablier correspond à l’addition des masses de tout les voussoirs du tablier multipliée par la constante gravitationnelle, qui est de 9.81 N/kg pour la France. L’origine du vecteur directeur du poids se trouve au milieu du tablier, de direction verticale et orienté vers le bas. Le poids du pilier : Le poids du pilier se calcul par la multiplication de sa masse par la constante gravitationnelle. L’origine du vecteur directeur du poids se trouve en son centre d’inertie, de direction verticale et orienté vers le bas. Cette force n'agit pas sur l'ensemble de la structure puisqu' elle crée sur le pylône une force de compression qui le solidifie. Formule : P = mg
|
Les forces qui s'appliquent au pont suspendu sont identiques au pont à haubans, en effet le pont à haubans est un pont suspendu, les quelques différences sont que les forces ne se trouvent pas au mêmes endroits.
La plus grande différence est que les forces de tension du pont suspendu ne sont pas les forces à l'origine directe de l'équilibre de la structure.

les ponts suspendus :
Le ponts suspendu est un pont qui permet le passage de nombreux véhicules tout en permettant le passage de bateaux en dessous du tablier. Pour pouvoir faire passer de nombreux véhicules sur ce pont, il faut qu’il soit très résistant.
Tout d’abord, il faut élaborer un tablier qui parcourt une longue distance. Une unique plaque de béton ne serai pas la bonne méthode car elle ne supporterait pas les grandes distances, elle se briserait sous le poids des véhicules
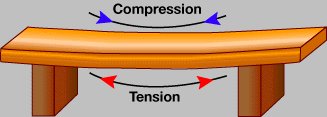
C’est à ce moment que le béton précontraint intervient, ce type de béton est très résistant sur des petites surfaces. Les ingénieurs de l’époque ont alors décidé de coller côte à côte ces plaques de béton précontraint.
Ces plaques reposent sur des voussoirs qui sont leurs supports. Touts les voussoirs sont relié les uns aux autres pour former une unique plaque très résistante. Le tablier admet alors une très grande solidité et permet le passage de grandes charges.
Animation
Seulement les points d’applications entre les 2 voussoirs doivent être soutenus, les ingénieurs ont décidés de mettre en place des câbles pour supporter leurs poids.
Tout ces petits câbles sont reliés à un unique câble porteur, il regroupe tout le poids du pont.
Le câble porteur est ensuite soutenue par 2 pylônes.
Mais les piliers ne sont pas assez résistants pour soutenir eux seul, tout le poids du pont.
Les ingénieurs ont alors décidé de prolongé le câble porteur sous terre et de l’accrocher à un bloc d’ancrage qui peut supporter de très grandes forces. Ce bloc consiste à compenser toute les forces qui sont mises en jeux.
Enfin, dans un pont suspendu comme dans un pont à haubans, il faut que la somme des moments (forces perpendiculaires à l'axe principal d'une pièce ) soit nulle et que les forces s'équilibrent en des forces de compression des piliers.
Calcul des forces :
Sur un pont suspendu à câbles porteurs
le poids du pont (tablier): P = mg
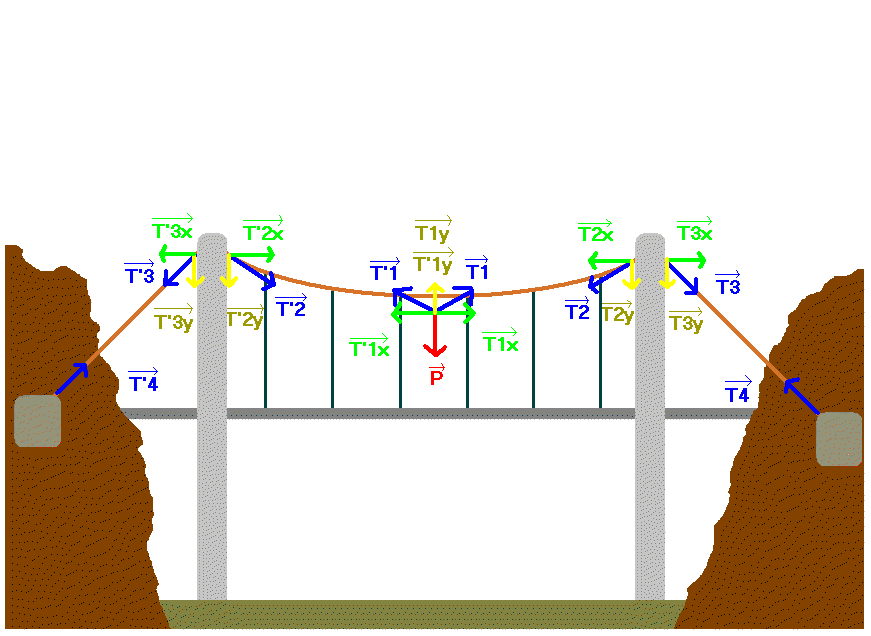
Globalement, le poids P total du pont se trouve au milieu du tablier, de direction verticale vers le bas. Cette force se compense par 2 tensions de même valeur T1, T2.
En détail, le câble orange supporte le poids du tablier par une multitude de petits câbles noirs verticaux. Le poids du tablier met en tension les câbles du pont. L
Il y a deux forces F, elles ont la même valeur, chacune d elle compense la moitié des forces totales du tablier.
Dans tout ponts suspendu la somme des forces doit être égale à 0 ainsi que la somme des moments
D'après la première loi de newton lorsque un système est en équilibre la somme des forces est nul
Dans le pont suspendu classique :
Le poids du tablier = Masse totale * constante gravitationnelle
Le poids crée 2 forces de tensions T'1 et T1.
Etant donné que le pont est symétrique est que les forces se repartissent de façon égale, nous nous occupons que d'un seul coté du pont.
.
Sur Ox = T1 * cos a = T1x
Sur Oz = T1 * sin a = T1y
T1 se compense avec T2, donc T2 +T1 =0
on décompose déjà T2 :
Sur Ox = T2 cos a = T2x
Sur Oz = T2 sin a = T2y
finalement,
Sur Oz T1x + T2x = 0
Sur Oz T1y + P = 0 ces deux vecteurs s'oppose et sont de même valeurs alors ils se compense
également T2y+ T3y + Pp + R = 0
en effet le poids du pylône Pp et T2y s'oppose à la réaction du sol R qui forme le vecteur nul
Ensuite on retrouve le même principe avec T3 et T4 puisque sans ces 2 forces, la somme de tout le système serai nulle mais pas la somme des moments, en effet les pylônes s'écrouleraient.
Sur Ox T3 *cos a = T3x
T4 *cos a = T4x
T4x +T3x = 0
Enfin sur Oz
T2y+ T3y + Pp + R = 0
en effet le poids du pylône Pp, et les tensions T2y et T3y s'oppose à la réaction du sol R qui forme le vecteur nul
Pp = masse du pylône * constante gravitationnel
les ponts à haubans :
Le pont à hauban est un pont intégrant aux ponts suspendus mais qui est totalement en équilibre. Il est apparu bien après le pont suspendu classique à cause du progrès technique et des nouveaux matériaux.
Le principe du pont à hauban est que sa structure est totalement en équilibre.
Tout d’abord, il y a un point d’équilibre au niveau du pilier où supporte le tablier.
On pose ensuite en même temps des voussoir de chaque coté du pylône pour former petit à petit le tablier en reliant chaque point d’application entre 2 voussoirs au pylône par des câbles.
Ces câbles se nomment les haubans, ils sont directement reliés du pylône au tablier.
L’avantage du pont à hauban est qu’il n’a pas besoin de point d’ancrage, on peut donc le construire plus facilement sur des zones planes, les ponts d’ancrages devant être enfuis dans le relief à proximité.
Mais la subtilité du pont à hauban est de mettre en tension les hauban en effet lorsqu’on décompose la forces de tension au niveau du tablier verticalement et horizontalement , la force verticale de cette tension est bien supérieure au poids du tablier, ainsi les véhicules sont supporté par la différence de la décomposition de la tension vertical et le poids du tablier.
le poids du pont (tablier): P = mg
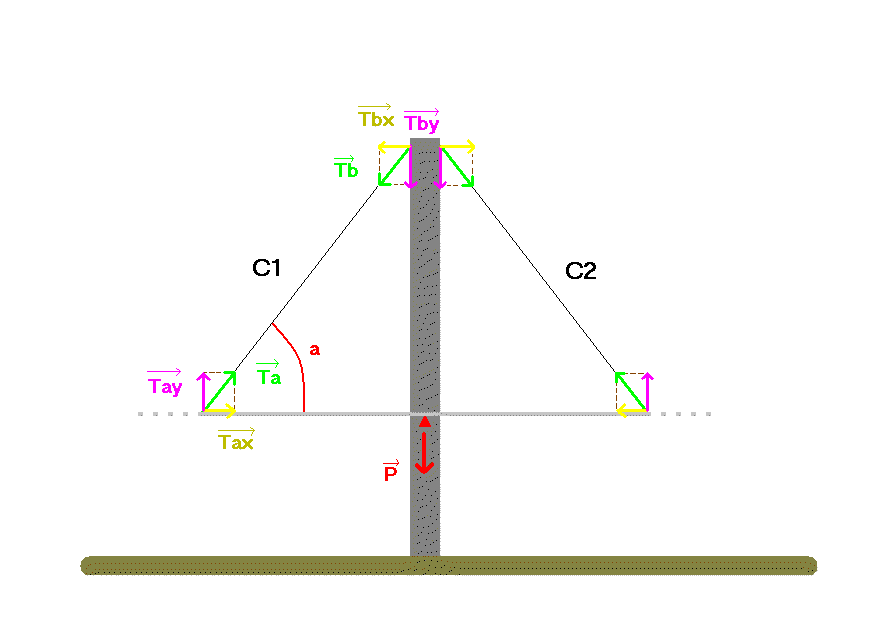
les tensions Ta et Tb.
Soit a l’angle formé par les câbles C1 et C2 avec le tablier.
Le tablier étant en équilibre, la somme des forces est nulle :
Fext = 0
Ici : ?Fext = Mg + Ta + Tb
On projette les vecteurs Ta et Tb dans un repère orthonormé [repère (O ;i ;j) :
Sur l’axe (O,x) : Tax + Tbx + Px = 0
Sur l’axe (O,y) : Tay + Tby + Py = 0
Or Px = 0 d’où Py =Mg
Ta a pour abscisse Ta * (cos a) et pour ordonnée Ta* (sin a) ;
Tb a pour abscisse Tb * (cos a) et pour ordonnée Tb* (sin a) ;
On obtient donc :
sur l’axe (O,x), on obtient : Ta * (cos a) +Tb* (cos a) = 0 ;
sur
l’axe (O,y), on obtient : -Mg + Ta*(sin a) +Tb*(sin a) = 0 ;
Première équation :
Ta* (cos a) +Tb * (cos a) = 0
Ta* (cos a) = -( Tb * (-cos a)) = 0
D’ou :
Ta* (cos a) = Tb * (cos a)
Ta = Tb
Donc la norme des deux tensions est la même.
Deuxième équation :
Si F = Ta = Tb
-Mg + Ta * (sin a) + Tb * (sin a) = 0
2 Ta * sin a = Mg
2 Ta = Mg/ (sin a))
Ta = Tb = F = P/ ((sin a) * 2)
On définit la fonction f : a ? F
f(x) = Mg / ((sin a) *2)
Exemple
Par exemple, si le tablier ferai un volume de 5000 m³ de béton. La masse volumique du fer est de :
µ = 7 870 kg/m³. La valeur de la force de
gravitation g est de : g = 9,81 N/kg.
La valeur du poids est :
P = m * g
P = µ * V * g
| P = 7870 * 5000 * 9.8 P = 3,85 10^6 N soit 385 millions de newton
|
| Ta = 3,85.10^6 / 2 sin 40° Ta = 2,99.10^6N
|
Résistance à la rupture
| On sait que les câbles ont environ une
résistance de180 daN/mm². D'après l'unité de la résistance R, nous pouvons
dire que : R = F / S avec F la force maximale applicable au câble et S la surface du câble en un point : le point central. Prenons un diamètre de câble de 50cm. |
| F = R * pi * r² F = 1800 * pi * 250² F = 3,53.10^6 N Soit environ 350 millions de Newton La force maximale applicable à ce pont suspendu est d'environ 350 millions de Newton. Pour donner un ordre de grandeur, un kilogramme exerce sur un autre corps une force de dix Newtons. Il faudrai donc une tres grande force pour rompre ce cable. |